『图灵完备』完全攻略之基础逻辑电路（一）

原力觉醒

只是想教会你如何连接导线

与非门

这一关要求玩家测试得出与非门（NAND）的真值表。什么是真值表？真值表其实就是输入和输出的对应关系。输入可以不止一个，在不同逻辑下，相同的输入可能会得到不同的输出。真值表可以让我们更直观地看出不同的逻辑关系。比如下图就是游戏中给出的与门（AND）的真值表。

回到这个关卡，题目已经给了我们与非门，我们只需要测试不同输入的情况下输出的情况，写在下方核对即可。

过关后，游戏告诉我们，利用这个元件可以造出电脑里的所有东西。

非门

非门就是我们常见的NOT，取反。题目要求我们利用与非门来搭建一个非门。

与非门有两个输入，但是非门只有一个输入。对比与非门的真值表我们可以很容易得出，当两个输入都是低电平的时候，输出为高电平，反之则为低电平。所以我们只要把输入同时给到与非门的两个接口，我们就能得到符合非门真值表的电路了。

与门

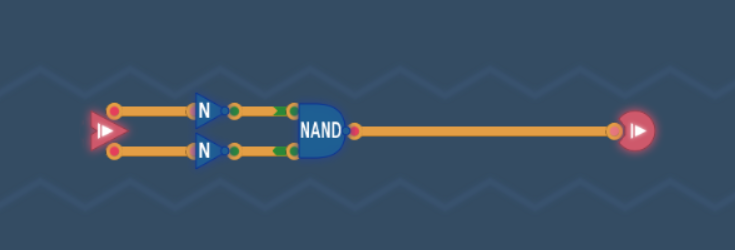
这个逻辑我们很熟悉，AND。问题在于我们现在只有与非门和非门可以用。仔细观察与非门和与门的真值表可以发现，它们的输出完全反过来。所以我们只需要在输入给到与非门后取反即可。

与门的性质就是，全真才为真。而与非门就可以理解为，与后非，即全假才为真。

或门

或门也是我们熟悉的OR，有真即为真。我们对比一下与非门和或门的真值表，会发现他们的输出刚好左右对称。

这里就要引出数电中很基础的一个定理：德摩根定律。

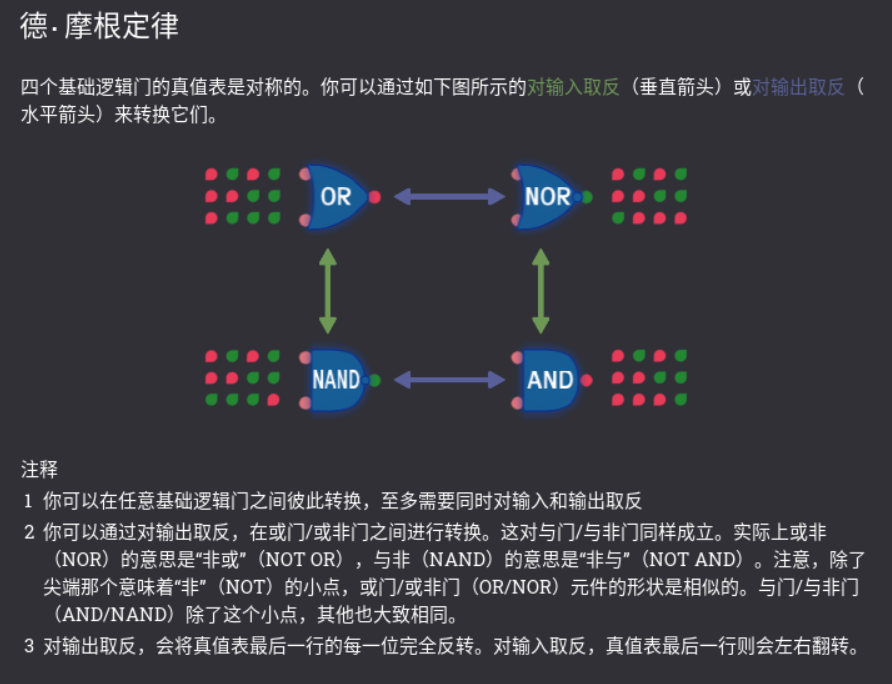
通俗点来讲就是，如果我们在输入的时候就取反，那么输出就会呈左右对称。如果我们在输出取反，那么输出会分别取反。回到这道题，我们只需要在与非门的输入（元件左边）取反，就能得到或门。

或非门

NOR，类比一下与非门的命名逻辑，显然或非门就是或后非。所以只要在或门后面的输出加上非门即可。这也是为什么前面先讲了或门，才来讲或非门。

高电平

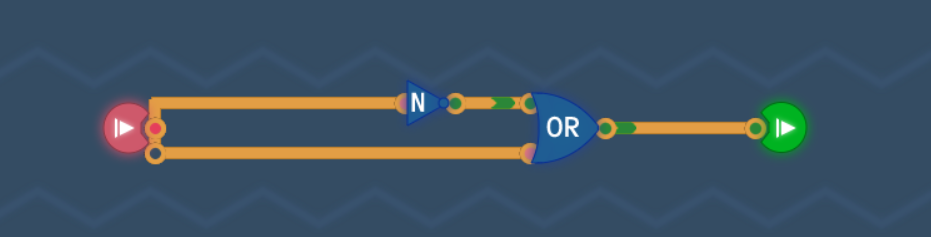
题目要求无论是输入是什么，输出时钟需要保持高电平（即为1）。很显然在只有一个输入的情况下，我们需要将其分为两条路子来给到元件，但是尽管是两条路也肯定没法保证全部都是高电平，但是可以轻松做到一个高电平一个低电平。我们利用或门（或者与非门）的性质就能永远输出高电平了。（解法不止一种）

第二刻

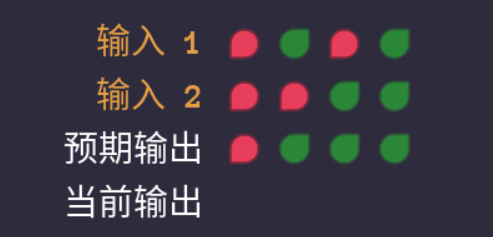
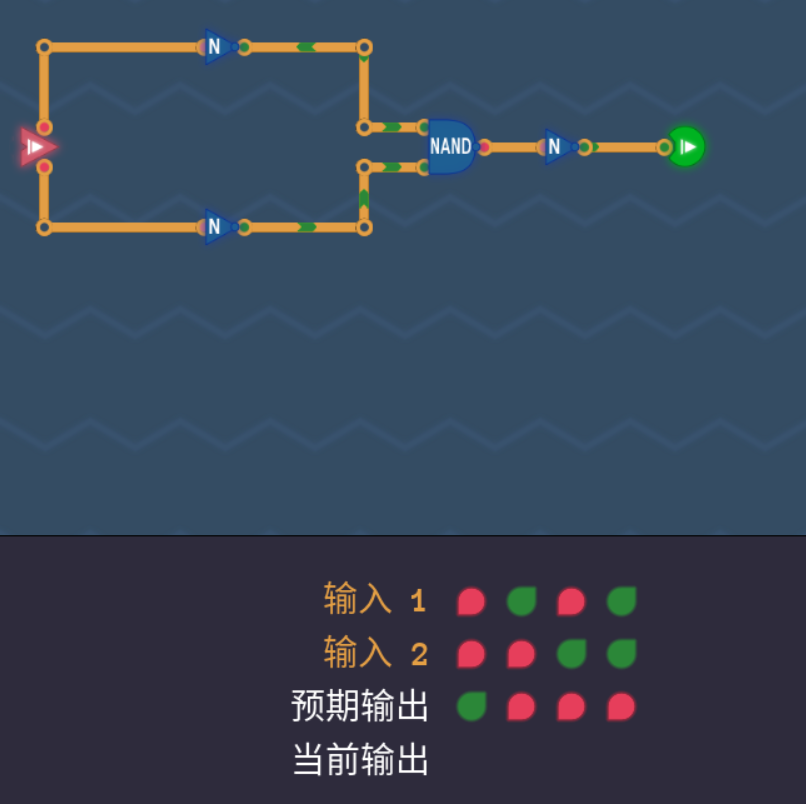
这道题其实有一种对着答案出题的感觉，其实完全不用管第几刻的问题，直接对着给出的真值表造就行。

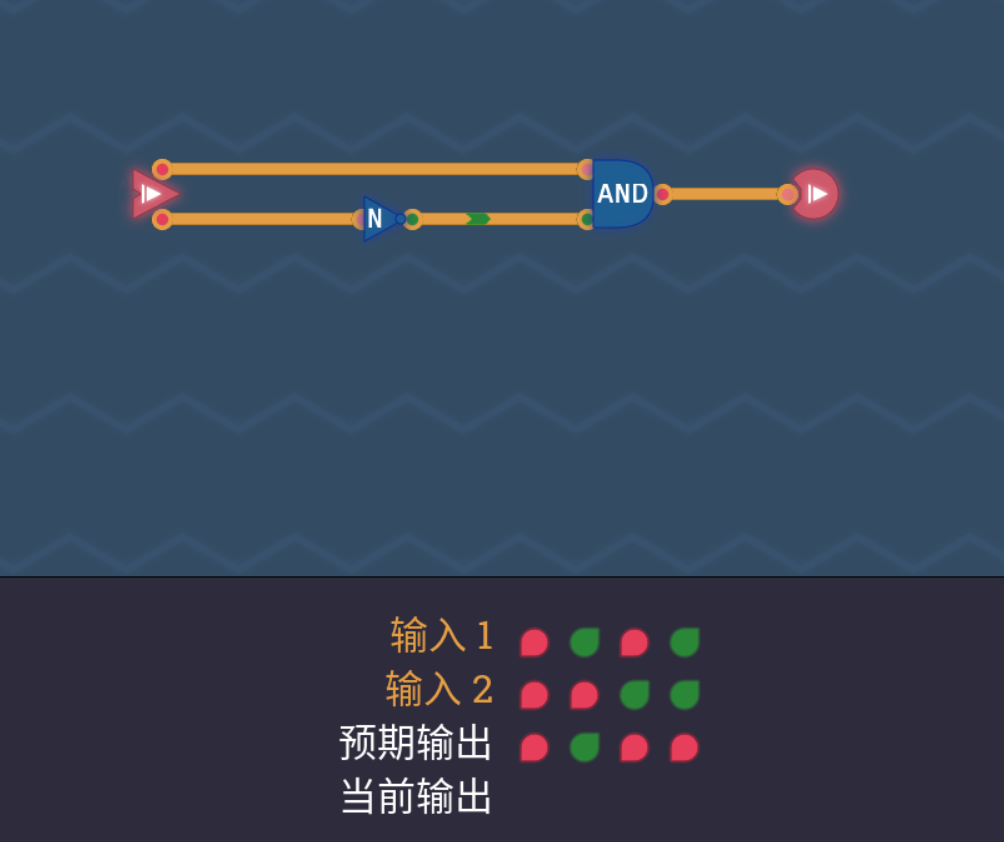
也不难发现，试想如果将真值表中输入2的值全部倒转会发生什么，那就变成与门的真值表了！所以我们只需要在输入2处加个非门即可。举一反三，如果下次要第三刻怎么办？诶！想想摩根定律。

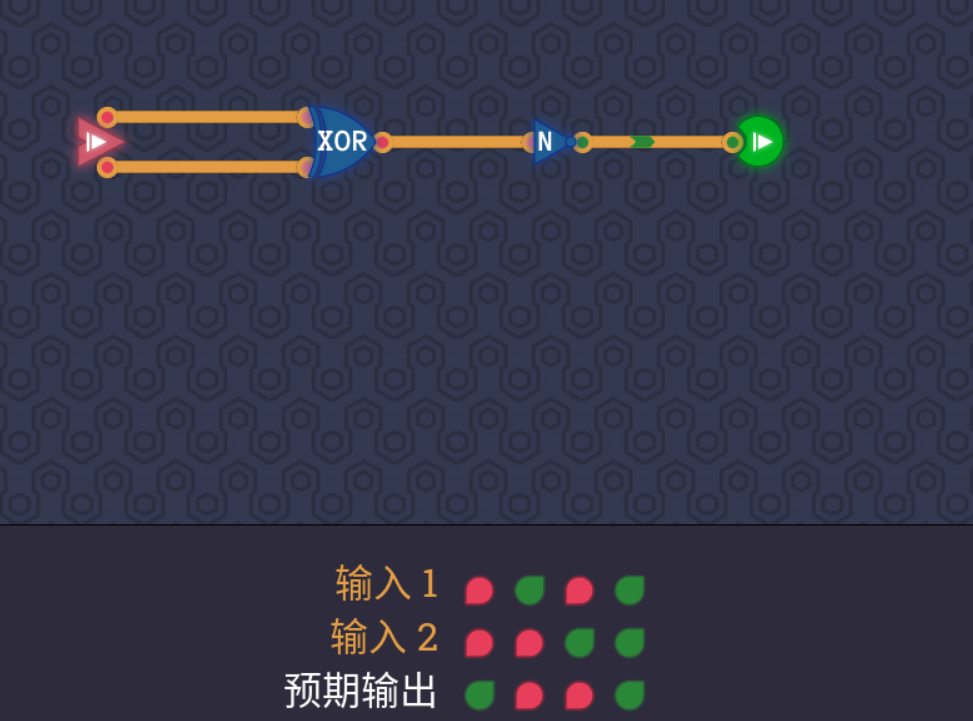
异或门

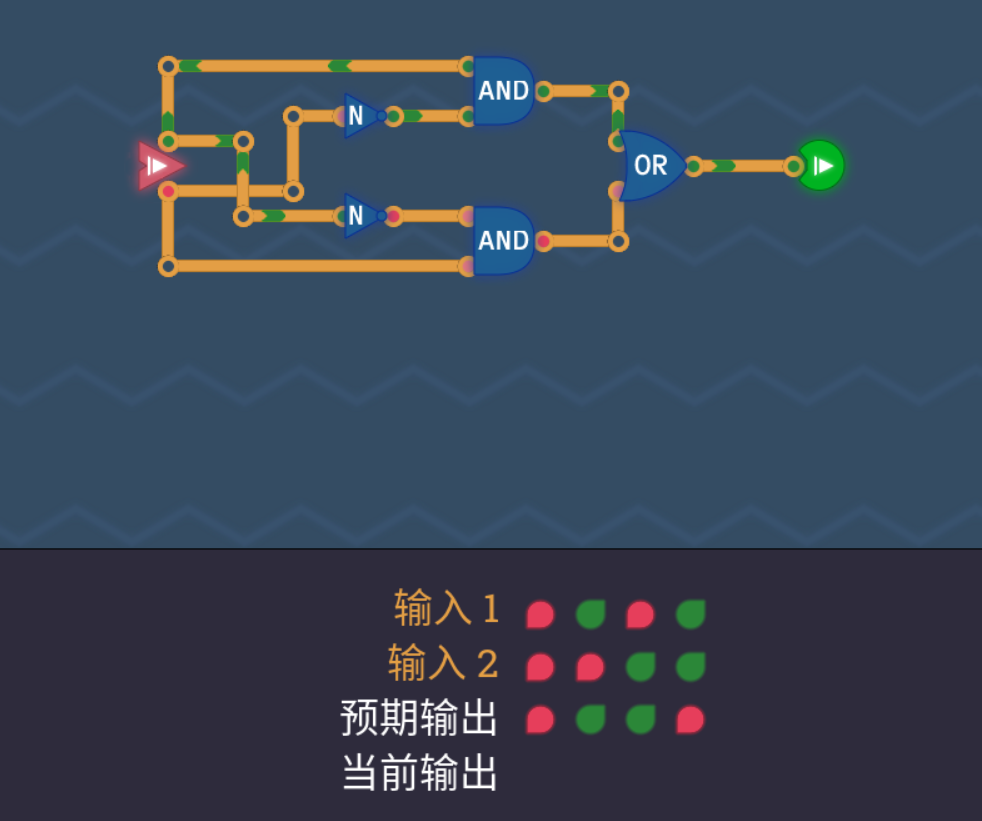
XOR，但是只能用前面见到过的元件。有一说一，有点难想。我的视角是这样的：观察真值表会发现，除了真真得假之外，其他三项和或门的性质很像，于是想到最后可能要用到或门在输出的位置，那么现在问题就转变成了如何在两个都为真的时候，让进入或门的两个输入都变成低电平。

我们现在抛弃其他的不想，我们就抓着或门的其中给一个输入来考虑。如果两个输入中一个接一个非门，然后接入与门，是不是就能实现两个输入为真的时候输出低电平？巧妙的是，当没接非门的那一个输入为真的时候，与门也能输出真，这不就符合了我们满足真真得假的设想。

三路或门

有一个真即为真，叠或门即可。

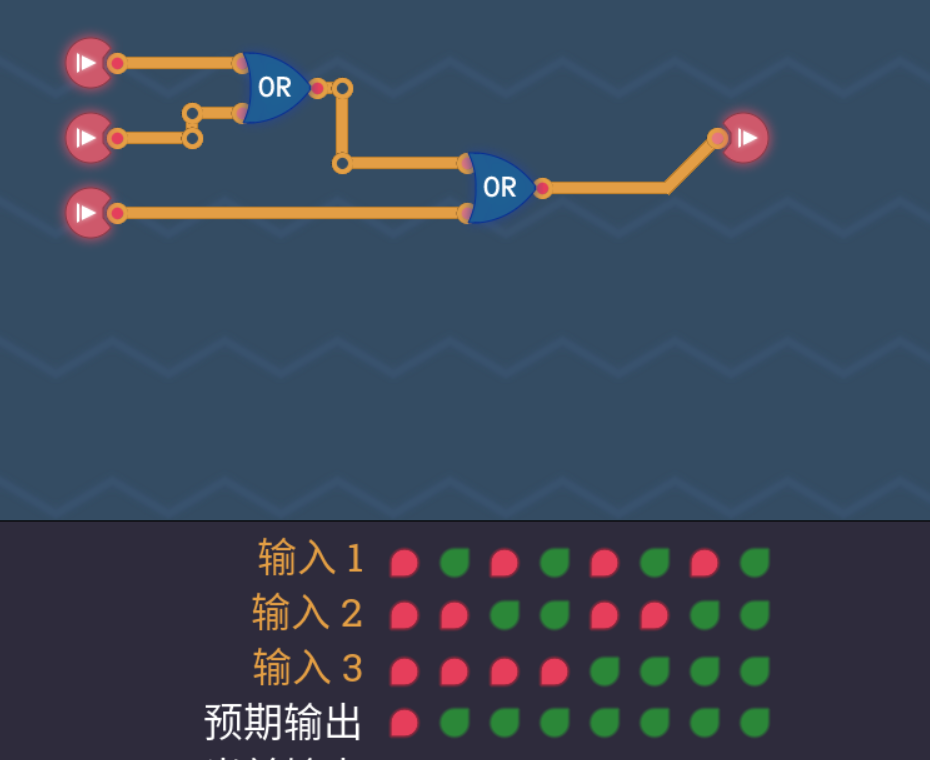
三路与门

全为真才为真，叠与门即可。

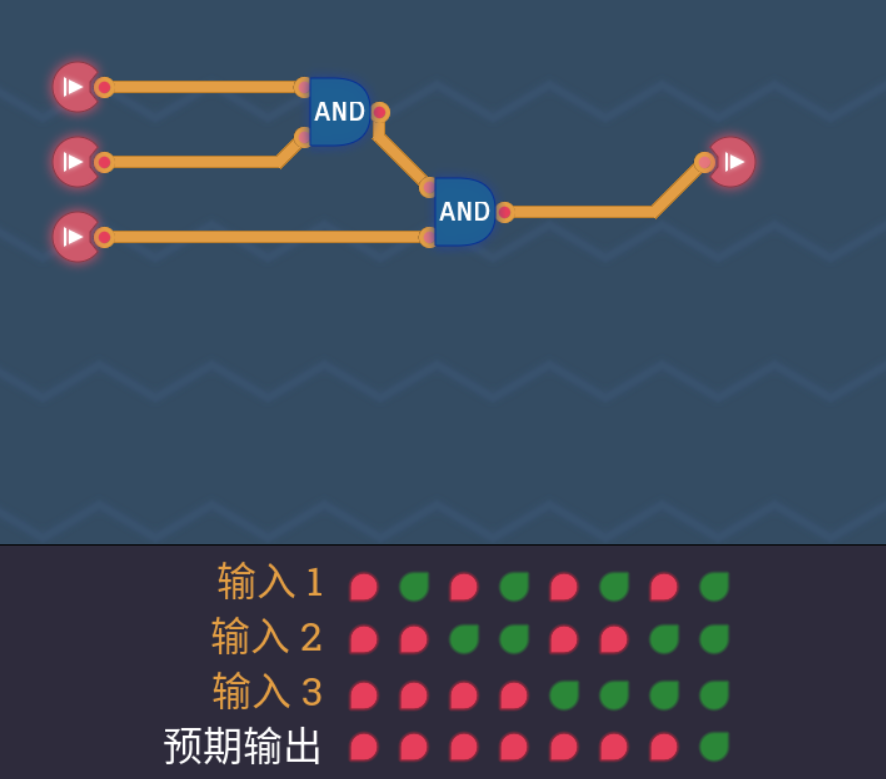
同或门

XNOR，真值表和异或门刚好反过来，根据摩根定律，在输出处加上非门即可。